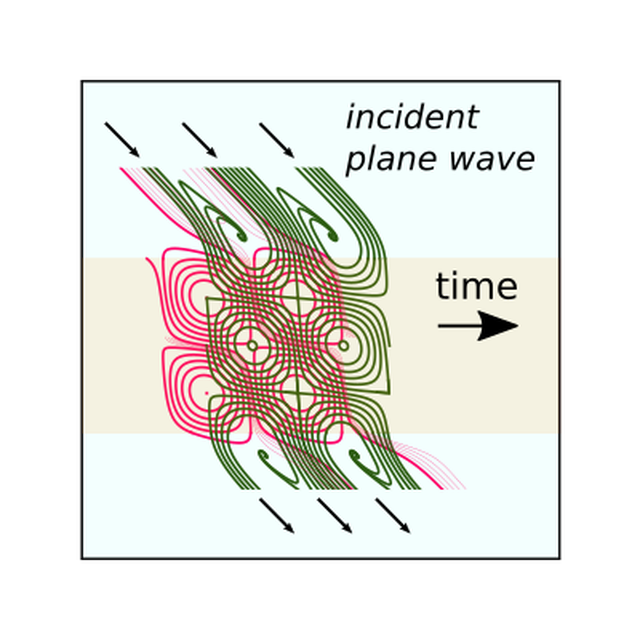
Depuis l'avènement des concepts relativistes einsteiniens, on considère que l'idée de lignes de forces, introduite par Faraday en 1852, ne devait plus être considérée que comme une illustration, qui ne résiste pas à un changement de référentiel. Feynman lui-même considéra dans son célèbre cours que le champ électromagnétique devait nécessairement être traité de manière abstraite. Mais ce n'est pas le cas ; en nous restreignant à une situation qui peut être visualisée aisément dans un espace (t,x,z) (un système invariant en y, polarisé p) nous pouvons construire dans la carte de l'espace-temps des lignes absolues, que nous nommons spaghettis électriques.
Le champ électromagnétique, alors habituellement décrit par ses trois composantes Hy, Ex, Ey, est complètement décrit par la topologie de ces spaghettis, avec une mesure, le paramètre caractéristique η, qui est nouvel invariant de Lorentz.
Contrairement à la ligne d'univers d'une particule, qui est toujours de type temps, les spaghettis électriques transcendent la distinction entre temps et espace, et le paramètre caractéristique η reste une mesure scalaire jamais nulle, même lorsque les spaghettis suivent des lignes nulles (les lignes du cône de lumière).
Lors de la transmission extraordinaire dans un réseau de fentes résonnant, on observe plusieurs structures topologiques intéressantes : des lignes droites dans la zone des ondes planes, des losanges arrondis dans la zone des fentes, sujette à interférence de deux ondes planes, et des structures fractales dans la zone de funneling (effet entonnoir) où l'onde incidente interfère avec les ondes évanescentes. Ces structures fractales, présentes dans le plan central, sont des spirales logarithmiques, la spira mirabilis de Bernouilli. Elle sont centrées sur les événements de champ nul et semblent contredire le sens commun qui, puisqu'il n'y pas de charge magnétique au centre, n'accepte pas qu'elles se terminent là. Mais, tout à la fois, elles ne se terminent pas - puisqu'elles sont fractales -, et les tubes de flux magnétique qu'elles supportent sont de mesure nulle.
Référence :
Lorentz-invariant topological structures of the electromagnetic field in a Fabry-Perot resonant slit grating
Marina Yakovleva, Jean-Luc Pelouard, and Fabrice Pardo, Phys. Rev. A 106, L060201
DOI : https://doi.org/10.1103/PhysRevA.106.L060201