Since the einsteinian relativistic concepts, it is considered that the idea of lines of force, introduced by Faraday in 1852, should only be considered as an illustration, which does not resist to a change of the reference frame. In his famous lectures, Feynman himself considered that the electromagnetic field should necessarily be treated in an abstract way. But this is not the case; by restricting ourselves to a situation that can be easily visualized in (t,x,z) space (a y-invariant, p-polarized system) we can construct absolute lines in the space-time map. We call these lines electric spaghettis.
The electromagnetic field, usually described by its three components Hy, Ex, Ey in a frame of reference, is completely described by the absolute topology of these spaghettis, with one measure, the characteristic parameter η, which is new Lorentz invariant.
Unlike the worldline of a particle, which is always time-like, the electric spaghettis transcend the distinction between time and space, and the characteristic parameter η remains a never-zero scalar measure, even when a spaghetti follows zero lines (the lines of the light cone).
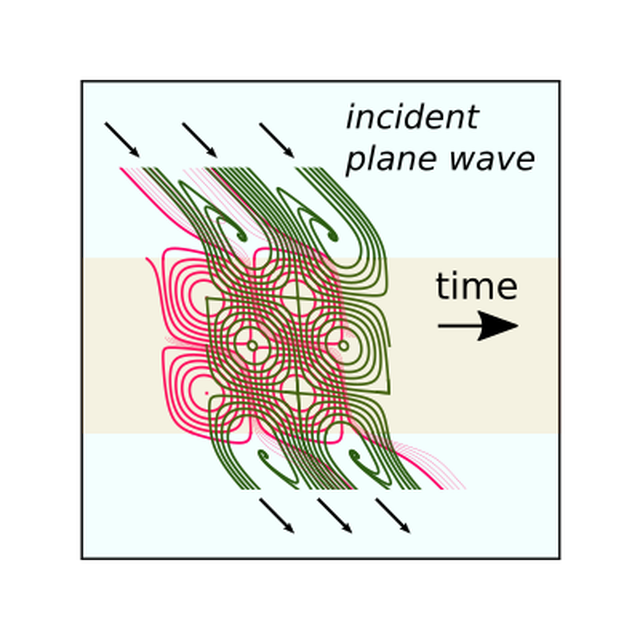
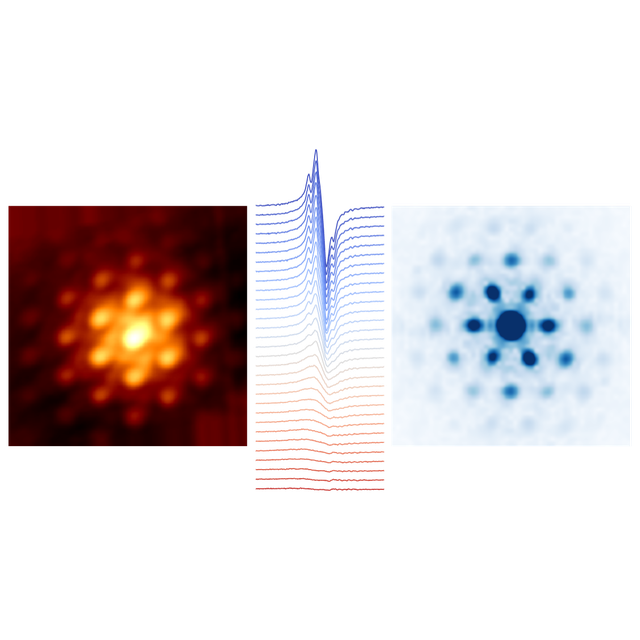
Extraordinary transmission in a resonant slit array manifests several interesting topological structures of the electric spaghettis: straight lines in the plane wave region, rounded diamonds in the slit region subject to the interference of two plane waves, and fractal structures in the funneling region where the incident wave interferes with the diffracted evanescent waves. These fractal structures, presenting in the central plane, are logarithmic spirals, the Bernouilli's spira mirabilis. They are centered on zero field events and seem to contradict common sense which, since there is no magnetic charge at the center, does not accept that they end there. But, at the same time, they do not end - since they are fractal -, and the magnetic flux tubes they support are of zero measure.
Reference:
Lorentz-invariant topological structures of the electromagnetic field in a Fabry-Perot resonant slit grating
Marina Yakovleva, Jean-Luc Pelouard, and Fabrice Pardo, Phys. Rev. A 106, L060201
DOI : https://doi.org/10.1103/PhysRevA.106.L060201