Researchers at C2N (CNRS/Université Paris-Saclay), PhLAM laboratory (CNRS/Univ. de Lille) and ETH Zurich have unveiled a novel mechanism describing how criticality - a phase in which waves are neither extended nor localized but in a so-called “critical state” - emerges in quasiperiodic structures. Combining experimental and theoretical work, their finding provides newinsight into the physics at the middle ground between order and disorder.

Quasiperiodic structures, which are ordered but are not strictly periodic, are the source of extraordinary beauty in nature, art, and science (butterfly wings iridescence, Islamic art, Penrose tiling, …). They are at the crossroads between periodic and randomly disordered systems. For physicists, quasiperiodic order is both aesthetically and intellectually appealing. Numerous physical processes, such as localization of classical and quantum waves, that are well described in periodic structures, fundamentally change their character when they happen in quasiperiodic systems. Writing in Nature Physics, an international team of researchers at the Centre de Nanosciences et de Nanotechnologies – C2N (CNRS/Univ. Paris-Saclay), at Phlam laboratory (CNRS/Université de Lille), and at ETH Zurich now describes combined theoretical and experimental work in which they explore wave localization in one-dimensional quasiperiodic structures. They discover a new mechanism by which criticality develops in such media.

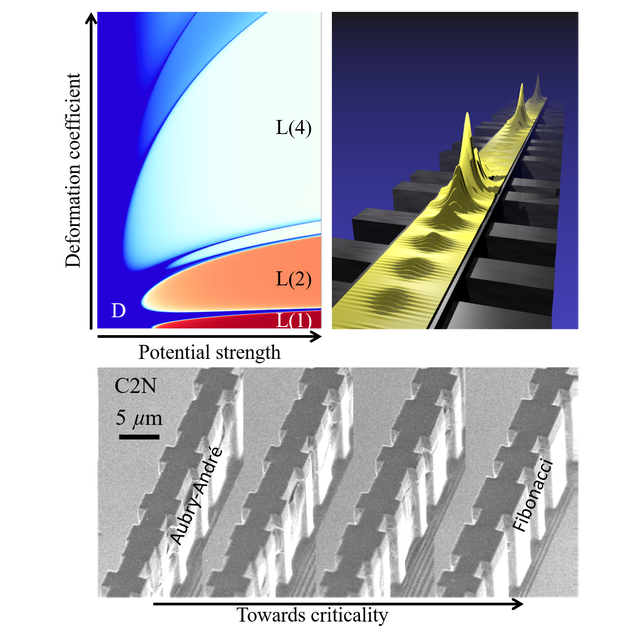
Two famous paradigmatic examples of quasi-periodic models are the Aubry–André and the Fibonacci models. Strikingly, they show very different localization properties. In the Aubry–André model, there are two distinct parameter regions in which waves can be in either ‘extended’ or ‘localized’ states (in the same sense as electrons can either propagate through a material or be stuck in an insulating state). At the boundary between these two regimes, waves are ‘critically localized’, showing a power law decay with self-similar features that are characteristic of fractality. By contrast, in the Fibonacci model, there is not one specific critical point separating two distinct regimes, but the waves are critically localized for any parameter of the system. Despite their sharply contrasting behaviours, the two models are connected, and can be continuously transformed into one another*. How such different localization behaviours are connected through this continuous transformation? This is the question that the researchers have answered in this work.

The C2N physicists had perfected a photonic platform** - so-called cavity-polariton lattices - in which light can be guided through semiconductor nanostructures while experiencing interactions similar to those acting on electrons moving through a crystal. Using the technological means at C2N, the researchers have fabricated with exquisite control photonic wires featuring quasiperiodic modulations in their width. This enabled them to implement experimentally, for the first time in any system, quasicrystals interpolating between the Aubry-André and the Fibonacci models. Optical spectroscopy experiments performed locally on these photonic quasi-crystals offer the invaluable advantage of being able to directly image light localization in the systems. At first sight, the structures shown in the figure look very similar. Surprisingly, the minimal differences implemented between these structures are sufficient to radically modify wave localization properties.

By combining their theoretical and experimental tools, the researchers were able to trace how the Aubry–André model evolves to become fully critical in the limit of the Fibonacci model. Counter naïve expectation, the team showed that this does not happen in a smooth way, but through a cascade of localization–delocalization transitions. Starting, for example, from the region of the Aubry–André model where waves are localized (dark red in the above phase diagram), at each step of the cascade process energy bands merge in a phase transition (blue streaks in the phase diagram), during which particles become delocalized. At the other side of the cascaded transition, the localization roughly doubles, sending the states of Aubry–André model gradually towards full criticality as it morphs into the Fibonacci model.

With this work, the researchers have provided an additional illustration of how powerful the polaritonic platform can be as a tool to tackle complex physical problems. The teams have successfully unveiled a general mechanism for the emergence of criticality in quasicrystals. The significance of these experiments goes firmly beyond light properties, as it also applies to the behaviour of electrons, atoms and other quantum entities that are governed by the same physics. In addition, this newly discovered mechanism is anticipated to inspire new ways of controlling conduction in quantum devices. Finally, the polaritonic quasi-crystals offer the potential to explore wave localization in presence of interactions, a topic of high interest linked to the recently discovered many-body localization.

* Y. E. Kraus and O. Zilberberg, “Topological Equivalence between the Fibonacci Quasicrystal and the Harper Model”, Phys. Rev. Lett. 109, 116404 (2012).
** A. Amo and J. Bloch, “Exciton-polaritons in lattices: A non-linear photonic simulator”, C. R. Physique 17, 934 (2016).

 

References:
Emergence of criticality through a cascade of delocalization transitions in quasiperiodic chains,
V. Goblot¹, A. Štrkalj², N. Pernet¹, J. L. Lado^2,3, C. Dorow¹, A. Lemaître¹, L. Le Gratiet¹, A. Harouri¹, I. Sagnes¹, S. Ravets¹, A. Amo⁴, J. Bloch¹ and O. Zilberberg²
Nature Physics, 2020
DOI: https://doi.org/10.1038/s41567-020-0908-7

1. Centre de Nanosciences et de Nanotechnologies – C2N (CNRS/UPSaclay)
2. Institute for Theoretical Physics, ETH Zurich, Switzerland
3. Department of Applied Physics, Aalto University, Finland
4. Laboratoire Physique des Lasers, Atomes et Molécules – PhLAM (CNRS/Univ. Lille), France

 

Contacts:

• Jacqueline Bloch, CNRS Senior Researcher at C2N
• Sylvain Ravets, CNRS Researcher at C2N

 

Figure: (top left): Calculated localization (L) and delocalization (D) phase diagram vs potential strength and quasicrystal deformation. The vertical axis origin corresponds to the Aubry-André limit (leftmost structure in the bottom Scanning Electron Microscopy (SEM) image), and asymptotically points towards the Fibonacci limit (rightmost structure in the bottom SEM image). Colors in the phase diagram encode the extent of the waves from fully delocalized (D – dark blue) to fully localized on one lattice site (L(1) – dark red). Intermediate shades of color L(N) represent waves that are localized on N lattice sites. (top-right): artistic view of a critical mode. (bottom): SEM images showing four different polaritonic structures used in the experiment to explore the phase diagram. The two central structures correspond to interpolations between the Aubry-André and Fibonacci models / Credits SEM images: C2N