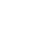The discovery of topological phases of matter, which was awarded the 2016 Nobel Prize in physics, has profoundly impacted our understanding of condensed matter. The hallmark of these topological phases is the existence of surface states whose properties can be completely insensitive to local perturbations. One of the most famous example of such topological states are the electrical conductivity plateaus measured in two-dimensional materials subject to strong magnetic field, a well-known phenomenon called the integer quantum Hall effect. The extreme robustness of these plateaus, which is harnessed in several metrology protocols, is directly linked to a fundamental quantity in topological physics called a “topological invariant”.
These topological invariants, which are a global property of a material, can be seen as the DNA of a topological phase, its mathematical signature. However, they are usually infer indirectly through local measurements at the edges of a sample, e.g. by probing the existence (or not) of topological states. This is a major drawback in many cases where the surfaces of a sample are dirty or difficult to probe. Researchers from the Centre for Nanosciences and Nanotechnologies, in collaboration with colleagues from PHLAM in Lille and from ICFO in Barcelona, have demonstrated a novel scheme allowing to directly measure these topological invariants from the bulk of a sample. Their results have been published in Physical Review Letters.
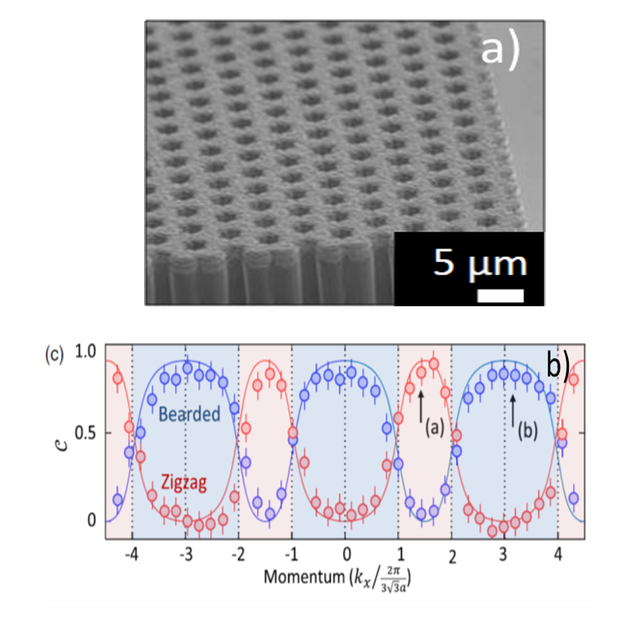
To do this, they used a photonic platform that emulates the physics of graphene, a material whose topological properties are well-known. In this platform, built by coupling semiconductor-based micropillars (see Figure a)), photons propagate similarly as electrons do in solid-state graphene. The technique developed by the researchers consists in generating a localized wave-packet and probing its propagation by collecting photons that escape the micropillars. Then, by doing a simple mathematical operation on the measured spatial profile, they were able to extract with a high accuracy the value of topological invariants that characterize the energy bands of this analog graphene lattice, which are related to the existence of edge states (see Figure b).
These results offer a new path for measuring fundamental topological properties of matter, directly from the bulk of a material. This technique could thus be extended to more exotic systems in order to identify and characterize the emergence of new topological phases.
Références
P. St-Jean1, A. Dauphin2, P. Massignan2,3, B. Real4, O. Jamadi4, M. Milicevic1, A. Lemaître1, A. Harouri1, L. Le Gratiet1, I. Sagnes1, S. Ravets1, J. Bloch1, and A. Amo4
Phys. Rev. Lett. 126, 127403
DOI:https://doi.org/10.1103/PhysRevLett.126.127403
Affiliations
1 Centre de Nanosciences et de Nanotechnologies (C2N), CNRS—Université Paris-Sud/Paris-Saclay, Palaiseau 91120, France
2 ICFO-Institut de Ciencies Fotoniques, The Barcelona Institute of Science and Technology, Avinguda Carl Friedrich Gauss 3, 08860 Castelldefels (Barcelona), Spain
3 Departament de Física, Universitat Politècnica de Catalunya, Campus Nord B4-B5, 08034 Barcelona, Spain
4 Univ. Lille, CNRS, UMR 8523—PhLAM—Physique des Lasers Atomes et Molécules, F-59000 Lille, France
Contacts
Jacqueline Bloch
Sylvain Ravets
Caption : a) Electron microscopy image of an artificial graphene lattice formed from the coupling of semiconductor-based micropillars; Extracted values of the topological invariant for a zigzag and a bearded termination. For regions of the reciprocal space where this value approaches 1, graphene exhibits an edge state.