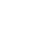When designing new electronics technologies, it is essential to be able to predict the results of experiments to optimize the technology and design systems that make use of it. For this purpose, a mathematical model of the technology is needed. Electronic devices are usually modeled by ordinary differential equations, which can be found by analyzing and understanding the underlying physics of the technology. However, this process can be difficult, and especially with the complex devices emerging from nanotechnology, is far from always being successful. In this work, we used a novel artificial intelligence technique, Neural Ordinary Differential Equations, to automatically create models of nanoelectronic devices. Based on a limited number of measurements, this technique can find an ordinary differential equation able to model the device in all situations without needing any physical insight. For example, we used this technique to model a spintronic nanoneuron, with highly complex behaviors that resist modeling. The resulting ordinary differential equation correctly predicted weeks of experimental measurements in only minutes of simulation. This work, which is generalizable to multiple physical systems, offers a new way to model and develop new technologies by benefitting from the recent progress of machine learning techniques.
This work involved multiple expertises and is a collaboration between researchers at Centre de Nanosciences et de Nanotechnologies, Unité Mixte de Physique CNRS/Thales, the Albert Fert Beijing Institute at Beihang University, and Université catholique de Louvain.
References
Forecasting the outcome of spintronic experiments with Neural Ordinary Differential Equations
Xing Chen1,2, Flavio Abreu Araujo3,4, Mathieu Riou4, Jacob Torrejon4, Dafiné Ravelosona2, Wang Kang1, Weisheng Zhao1, Julie Grollier4 & Damien Querlioz2
Nature Communications volume 13, Article number: 1016 (2022)
DOI https://doi.org/10.1038/s41467-022-28571-7
Affiliations
1Fert Beijing Institute, MIIT Key Laboratory of Spintronics, School of Integrated Circuit Science and Engineering, Beihang University, 100191, Beijing, China
2Université Paris-Saclay, CNRS, Centre de Nanosciences et de Nanotechnologies, Palaiseau, France
3Institute of Condensed Matter and Nanosciences, Université catholique de Louvain, Place Croix du Sud 1, Louvain-la-Neuve, 1348, Belgium
4Unité Mixte de Physique, CNRS, Thales, Université Paris-Saclay, Palaiseau, France
Figure : A Neural Ordinary Differential equation (a) is a specific type of artificial intelligence that can learn to model physical systems. For example, we trained a Neural Ordinary Differential equation to model an artificial nanoneuron (b). This trained equation can then predict of experiments on the nanoneuron with high precision (c).