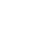Optical solitons are highly localized nonlinear states of light, which are named by analogy with solitary waves encountered in hydrodynamics. C2N researchers, with two teams one from the Phlam laboratory in Lille and the other from Institut Pascal in Clermont-Ferrand, have discovered a new family of optical solitons, stabilized by a continuous laser drive of the system, that enable modifying the topology of a one-dimensional topological array of semiconductor nonlinear microcavities. Remarkably, these solitons make possible the generation of an optical interface (an edge) in the bulk of the lattice.
Topology is a branch of mathematics that classifies objects independently of their local symmetries (the detail of their shape), by using global properties characterized by integers called topological invariants. These concepts have proven extraordinary in explaining the deep nature of certain physical phenomena such as the quantum Hall effect of a two-dimensional gas of electrons, in which electrical conduction occurs through edge channels localized at the interface between the material and vacuum. Fabricating synthetic physical systems allow extending the field of topological physics, and tackling one of the major challenges of the field: the influence of interactions on these topological phases. Nowadays, the field of photonics makes it possible to combine topology and non-linear optics. This is what C2N researchers have just achieved in collaboration with a team from the Institut Pascal in Clermont-Ferrand. They studied the non-linear response of a one-dimensional chain of optical resonators under continuous laser drive (see figure a). These chains consist of semiconductor cavities containing an active material (a quantum well) and operating in the strong exciton-photon coupling regime, thus leading to a giant optical non-linearity.
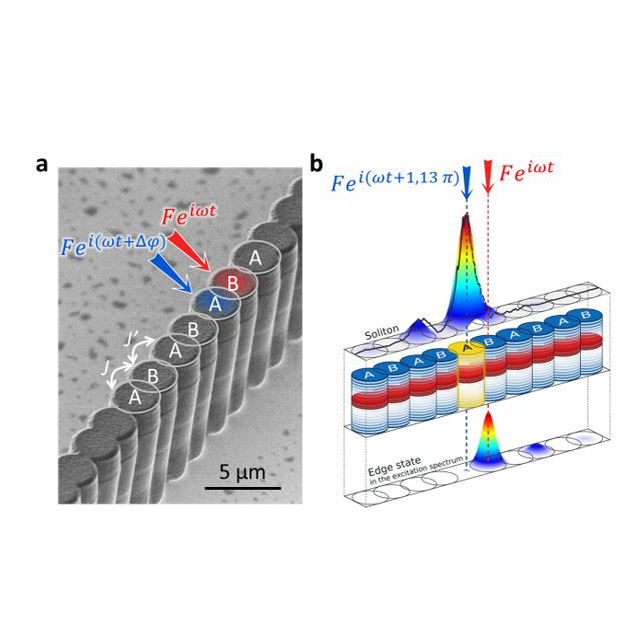
By imposing a phase frustration via the quasi-resonant continuous laser excitation, the researchers were able to stabilize a new family of dissipative solitons, which have no equivalent in conservative systems. These solitons inherit the symmetry properties of the lattice, which make them robust against certain types of defects. Remarkably, these new solitons show a peculiar spatial distribution, which optically "breaks" the chain, effectively removing one of the sites from the array (see figure b). This is a striking demonstration that interactions can be tailored to generate a new edge in the bulk of the lattice, and therefore to induce a new topological edge state at a completely unexpected location from the point of view of linear physics.
These results open up a new field of research aimed at manipulating the topology of an open system via the optical drive, a promising technique for the future study of the nonlinear properties of two-dimensional photonic topological insulators.
Références
Gap solitons in a one-dimensional driven-dissipative topological lattice
N. Pernet, et al.,
Nature Physics (2022)
DOI : https://doi.org/10.1038/s41567-022-01599-8
Topological interface of light
F. K. Kunst, News & views
Nature Physics (2022)
DOI : https://doi.org/10.1038/s41567-022-01582-3
Contacts :
Jacqueline Bloch
Sylvain Ravets
Caption : (a) Scanning electron microscopy image showing a chain of semiconductor cavities. The distance between the cavities is modulated, which gives rise to two different values of the coupling J and J’ between adjacent cavities (represented schematically by double white arrows). This modulation of the coupling provides the lattice with topological properties. Two cavities of the lattice are excited by two lasers of amplitude F, angular frequency w and presenting a phase difference Dj . b) For Dj =1.13p the researchers have demonstrated a new family of solitons, which measured intensity profile is shown at the top of the figure. The intensity is very strong on one single site, thus leading to the spectral detuning of this site with respect to the rest of the chain. The chain is thus effectively broken, and an edge state appears in the excitation spectrum, as shown at the bottom of the figure.